Networks in Edgy Activity Solutions

Sequencing in Edgy

Exercise 1

The nodes A and B will be shaped like circles, but the node C will be rectangular shaped. This is because the node C is added to the Graph after the set shape of all nodes to circle block and consequently that block has no effect on the node C.

To make all of the nodes shaped like circles, you would have to place the set shape of all nodes to circle block after the block that adds the node C. The corrected stack of blocks - which would make A,B and C shaped like circles - is shown in the below image.

Exercise 2

The Graph that results from that stack of blocks is shown in the below image.

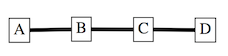
The Graph is connected, because there is a path from every node to every other node. The Graph is not cyclic (acyclic) because there are no cycles in the Graph.

Repetition in Edgy

Exercise 1

The resulting Graph will look like the image below.

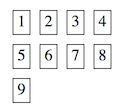
As you can see, there will be 9 (3 times 3) nodes in the Graph.

Exercise 2

The add edge block in the inner repeat block has a typo in the edge that is being added. Both of the nodes in the edge to add are the same (item i of all the nodes) and consequently Loop edges are added to the Graph. Instead the edge should connect item i of all the nodes and item j of all the nodes, so that there is an edge between each pair of nodes.

The corrected stack of blocks is shown in the image below:

Randomisation in Edgy

Exercise 1

The random Graph is pictured below.

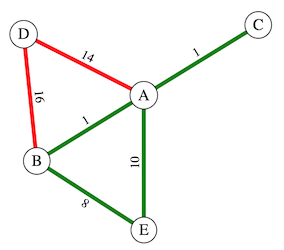
G_R contains the nodes: A,B,C,D and E, and the edges: (A,D) and (B,D). G_R is not connected, because there are no paths with red edges to the nodes: C and E. G_R is acyclic - it contains no cycles of red edges.

G_G contains the nodes: A,B,C,D and E, and the edges: (A,B), (A,C), (A,E) and (B,E). G_G is not connected, because there are no paths with green edges from D to any of the other nodes. G_G is cyclic, because it contains a cycle of green edges: (A,B), (B,E) and (E,A).

Exercise 2

The other random Graph is pictured below.

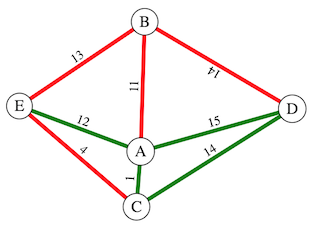
G_R contains the nodes: A,B,C,D and E, and the edges: (A,B),(B,E),(B,D) and (C,E). G_R is connected, because there is a path of red edges between each of the pairs of nodes in the Sub-Graph. G_R is acyclic, because there are no cycles in the Sub-Graph.

G_G contains the nodes: A,B,C,D and E, and the edges: (A,C),(A,D),(A,E) and (C,D). G_G is not connected, because there no paths with green edges from B to any of the other nodes. G_G is cyclic, because it contains a cycle of green edges: (A,C),(C,D) and (D,A).

Connected Graphs

Exercise 1

The Graph in the Check Your Understanding question is shown in the image below:

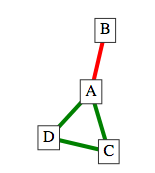
In the algorithm that we have created for finding whether a Sub-Graph with certain coloured edges is connected, it does not matter which node the algorithm starts from.

If the algorithm starts from B, then no other nodes will be added to the to visit Stack, because the only edge out of A is red. Consequently, only B will be in the visited List and the algorithm will report that the Graph is not connected.

If, however, the edge from B to A is green - then the Graph would be connected and the algorithm would report true.

The Random Graph Program

We have included pictures of what all of the blocks in the finished Random Graph program will look like. After completing the Coding in Snap! Activity, the blocks in your stack of blocks that follow the when green flag clicked block should look like this image.

The blocks inside the Block Editor for the is subgraph of colour edges connected block should look like this image

The blocks inside the Block Editor for the is subgraph of colour edges cyclic block should look like this image